Although statistics may seem straightforward at first glance, the learning curve can actually be quite steep. Understanding basic distributions is crucial in this regard. This article aims to provide a simple explanation of binomial distributions.

Flipping a coin is one of the simplest probability examples to understand, which is why many textbooks use it. If I flip a coin twice, the probability distribution looks like this:

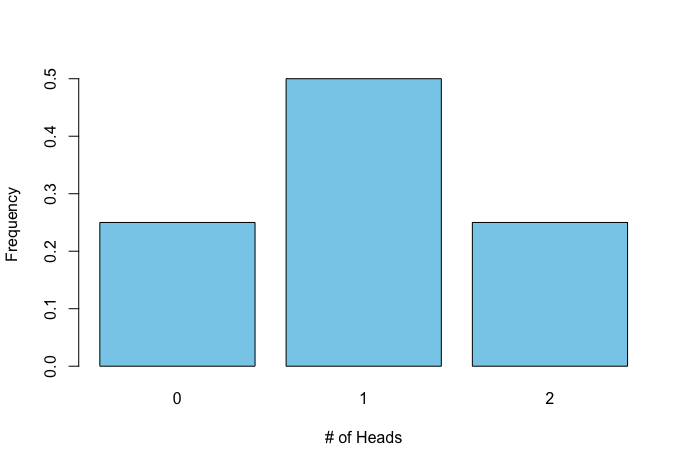
Let’s assume this represents the number of heads we get—since the probability is 50%, it doesn’t matter whether we choose heads or tails. The distribution indicates that the chance of getting no heads in our coin-flipping experiment is 25%, while getting one head has a 50% chance, and getting all heads and no tails is again a 25% chance. But what does this actually mean? Does it mean that if I flip a coin twice, I should get one head because that outcome has a higher chance? What if I repeat this experiment six times (each time flipping a coin twice)? Will I observe one head in half of the trials? I ran the experiment and plotted the results:

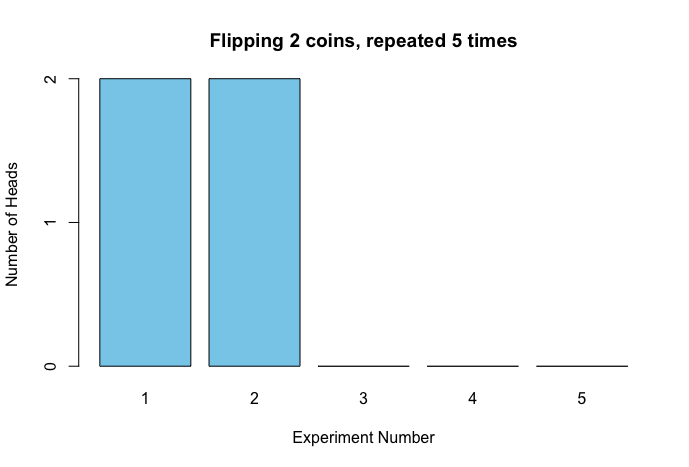
Well, it’s strange. I got two heads in the first two experiments, but no heads at all in the remaining three. I was supposed to get one head 50% of the time, but in my six experiments I didn’t get one head at all! What’s wrong here?

This outcome wasn’t unexpected. In fact, if you run the experiment, it’s unlikely you’ll get one head 50% of the time, especially when you repeat it only a small number of times like I did.

A binomial distribution represents a theoretical outcome. A theoretical outcome is what probability theory predicts should happen, based on a mathematical model, rather than what you actually observe in a real experiment. In other words, it shows what would happen if we ran the experiment an infinite number of times—the more we run it, the closer it gets to the theoretical outcome.

From a statistical view, this is what the word “chance” means. In a sci-fi world where you could split into infinite parallel worlds, and in each one you ran the coin-flipping experiment, you would see exactly one head in half of those worlds. If that had happened, theoretically, in one of those realities, you could find out how to communicate with other clones and verify the outcome.